https://www.acmicpc.net/problem/1041
1041번: 주사위
첫째 줄에 N이 주어진다. 둘째 줄에 주사위에 쓰여 있는 수가 주어진다. 위의 그림에서 A, B, C, D, E, F에 쓰여 있는 수가 차례대로 주어진다. N은 1,000,000보다 작거나 같은 자연수이고, 쓰여 있는 수
www.acmicpc.net
주사위의 6개의 눈과 N을 입력받으면, 해당 주사위로 이루어진
N×N×N크기의 정육면체의 5개의 면에 쓰여 있는 수의 합의 최솟값을 출력하는 문제이다.
처음에는 3면이 보이는 주사위 갯수, 2면이 보이는 주사위 갯수, 1면이 보이는 주사위 갯수를 구하고, 각각 주사위의 3면,2면,1면의 최소합을 구해 곱하면 되는줄 알았다.
운이 좋게도, 테스트 케이스는 다 통과했지만 "틀렸습니다"가 떴다.
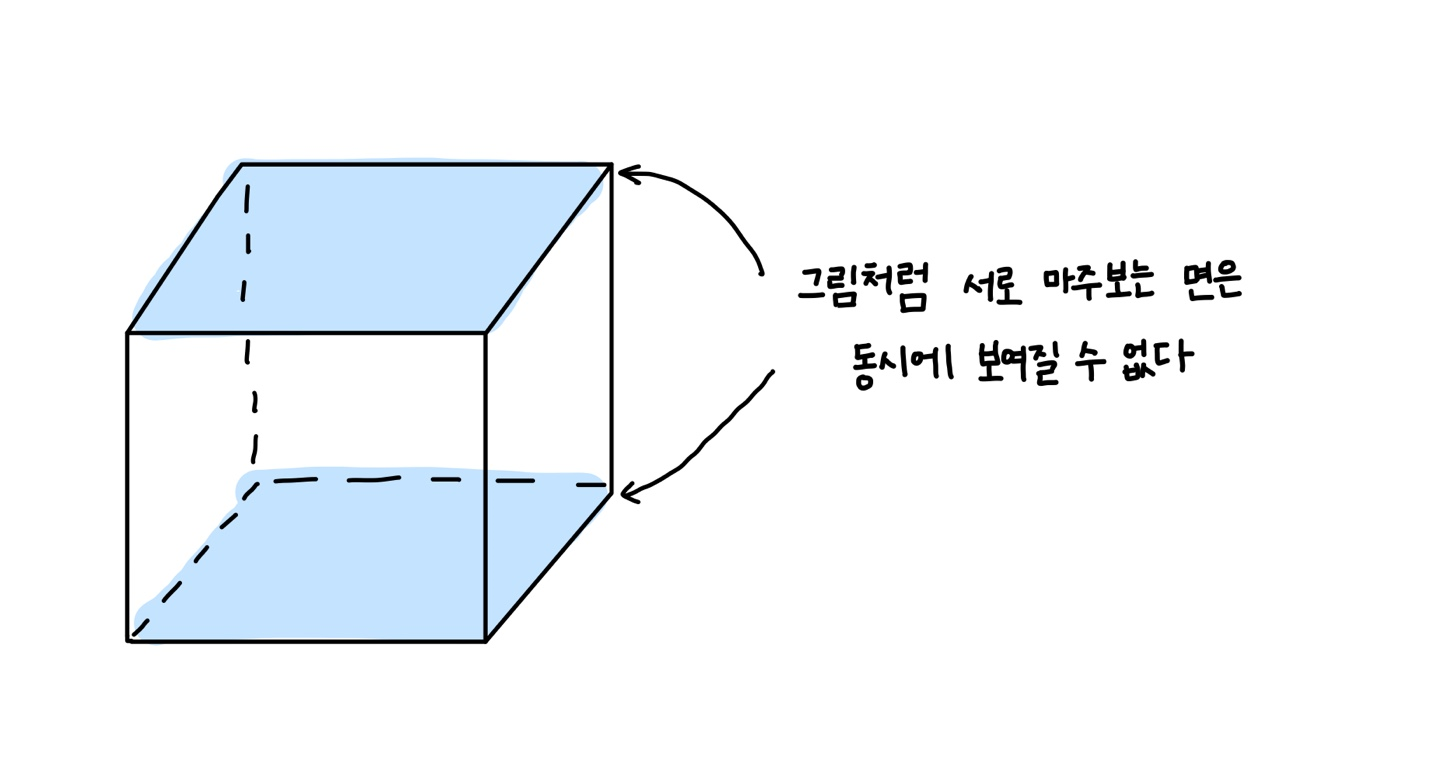
곰곰히 다시 생각해보니, 3면과 2면의 최소합을 구할 때는 마주보는 면이 포함되면 안된다. 그러면, 최소조합을 구할때 마주보는 면이 한개라도 포함되는 경우는 제외를 해줘야한다.
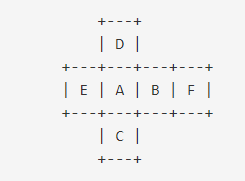
아래는 문제에서 나온 주사위 전개도고 입력은 A부터 차례대로 F까지 받는다. 마주보는 경우는 총 3가지로 인덱스를 생각해보면,
A-F (0-5)
C-D (2-3)
B-E (1-4)
이다. 즉, 0부터 입력받는 경우에 인덱스의 합이 5인 경우가 마주보는 경우이다.
따라서, 코드구현은 다음과 같이 하였다.
for (int i = 0; i < 6; i++){
one = min(one, v[i]);
for (int j = i + 1; j < 6; j++) {
if (i + j == 5) continue;
two = min(v[i] + v[j], two);
for (int k = j + 1; k < 6; k++) {
if (i + k == 5 || j + k == 5) continue;
three = min(three, v[i] + v[j] + v[k]);
}
}
}
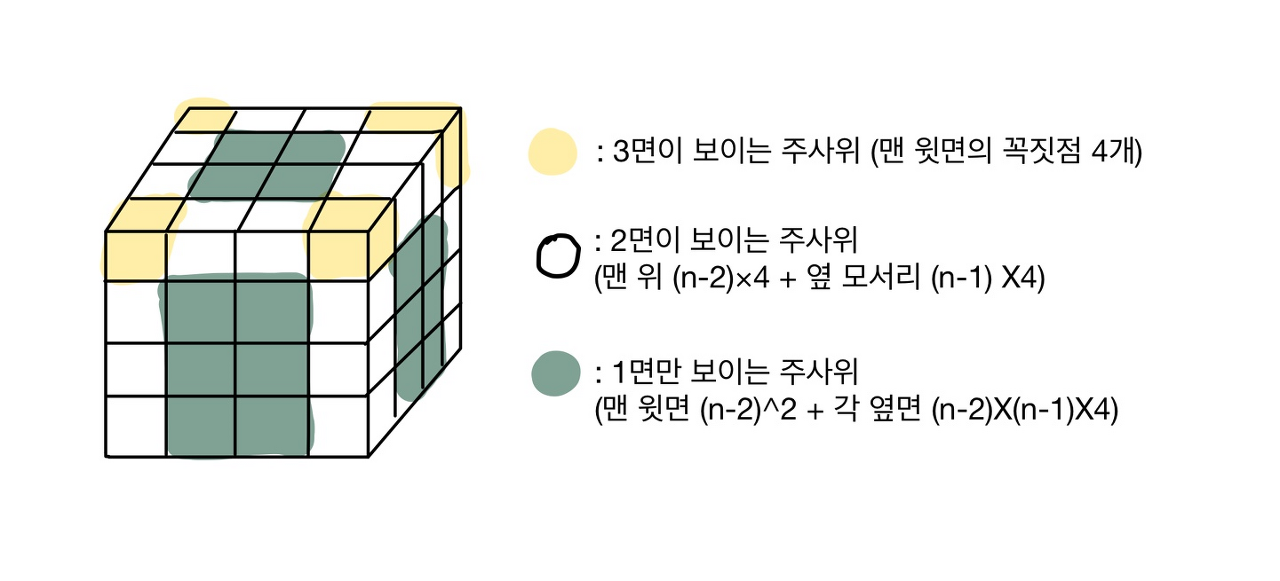
그리고, 아까 말했던 1면/2면/3면이 보이는 주사위의 갯수는 그림을 그려보면 금방 규칙을 찾을 수 있다.
풀어서 쓰면,
3면 : 4
2면 : 8N-12
1면 : (5N-6)(N-2)
이므로 1면 x one + 2면 x two + 3면 x three 를 통해 최종 답을 구할 수 있다.
단, N이 1인 경우는 예외 경우로, 눈의 총합에서 최대 눈을 빼준 값으로 처리하였다.
아래는 전체 코드이다.
하나 더 유의해야 했던건 처음엔 N을 int형으로 두었었는데 그렇게하면 마지막 result계산할때 N*N이 되면서 오버플로우가 난다. 따라서, long long으로 바꿔줘야했다. 자료형 선택때문에 틀린적이 많았는데, 이 부분에 대해 유의를 좀 해야겠다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
long long N, result;
vector<int> v(6); //주사위
int one = 5000, two = 5000, three = 5000; //1면,2면,3면 최소조합
int largest,sum; //가장 큰눈 , 눈의합
int main() {
cin >> N;
for (int i = 0; i < 6; i++) {
cin >> v[i];
sum += v[i];
largest = max(largest, v[i]);
}
//마주보는 조합만 피하기 (0,5) , (1,4) , (2,3) -> 인덱스 합 : 5
for (int i = 0; i < 6; i++){
one = min(one, v[i]);
for (int j = i + 1; j < 6; j++) {
if (i + j == 5) continue;
two = min(v[i] + v[j], two);
for (int k = j + 1; k < 6; k++) {
if (i + k == 5 || j + k == 5) continue;
three = min(three, v[i] + v[j] + v[k]);
}
}
}
//3면 : 4 , 2면 : 8N-12 , 1면 : (5N-6)(N-2)
if (N == 1) result = sum - largest;
else result = (4 * three) + ((8*N-12)*two) + (5 * N - 6) * (N - 2) * one;
cout << result << endl;
}
References
'Algorithm > 그리디' 카테고리의 다른 글
| [프로그래머스] 광고삽입 (C++) (2021 KAKAO BLIND RECRUITMENT) (1) | 2021.10.02 |
|---|---|
| [백준] 1647번 : 도시 분할 계획 (0) | 2021.09.24 |
| [백준] 1920번 : 수 찾기 (C++) (0) | 2021.09.21 |
| [백준] 1197번 : 최소 스패닝 트리 (C++) (0) | 2021.09.15 |
| [백준] 8980번 : 택배 (C++) (0) | 2021.09.05 |




댓글