복습
Spanning Tree
그래프 내의 모든 정점을 포함하는 트리를 의미한다.
Spanning Tree의 특징
- Tree의 특수한 형태로 모든 정점이 연결되어 있어야 한다.
- 하나의 그래프에 여러개의 스패닝 트리가 존재할 수 있다.
- 사이클이 존재하면 안된다.
- N개의 정점을 정확히 N-1개의 간선으로 연결해야한다.
Minimum Spanning Tree (MST)
사용된 간선들의 가중치 합이 최소인 Spanning Tree를 의미한다.
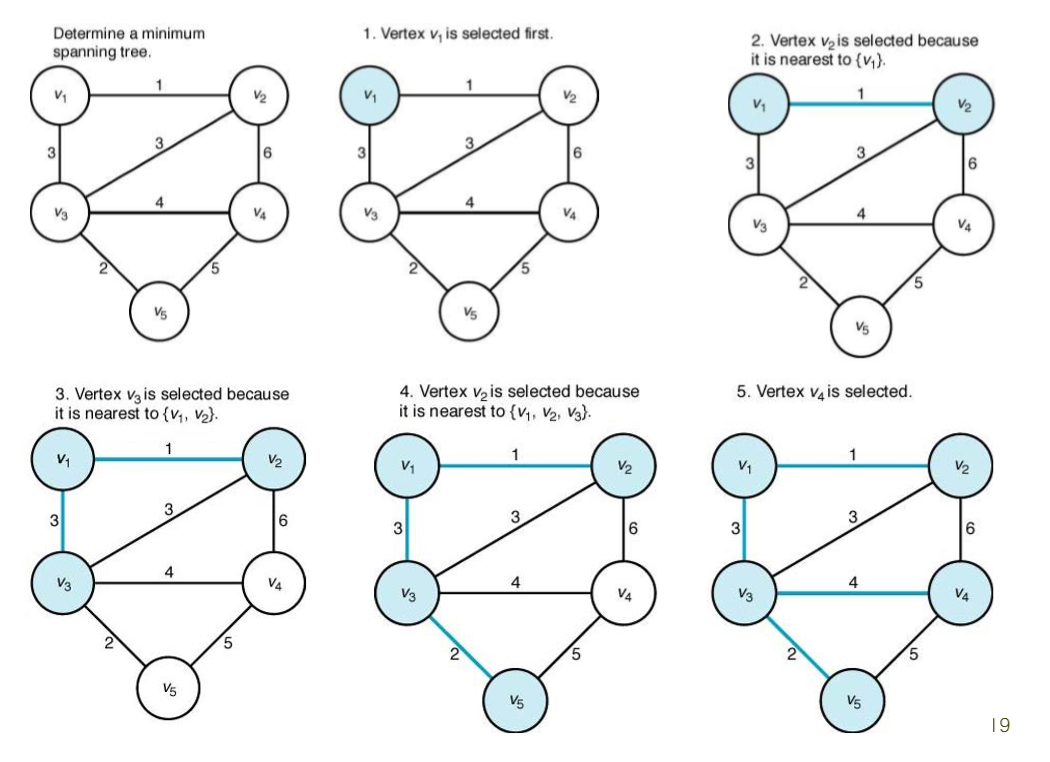
프림 알고리즘 ( Prim Algorithm)
무방향 그래프가 주어졌을 때 최소 스패닝트리 (MST)를 찾는 대표적인 알고리즘으로 시작 정점을 기준으로 가중치가 가장 작은 간선과 연결된 정점을 선택하며 신장 트리를 확장 시킨다
동작 방법
1. 임의의 정점을 선택 (어떤 정점에서 시작해도 같은 Tree가 나옴)
2. 인접 정점중 최소 간선으로 연결된 정점을 선택
3. 모든 정점이 선택될 때까지 반복
Prim 알고리즘의 시간복잡도
평균 : O(nlogn)
최악 : O(n^2)
크루스칼 vs 프림
- 크루스칼은 간선 위주의 알고리즘, 프림은 정점 위주의 알고리즘
- 프림은 시작점을 정하고, 시작점에서 가까운 정점을 선택하면서 트리르 구성 하기 때문에 사이클 검사가 필요없지만 크루스칼은 시작점을 따로 정하지 않고 최소 비용의 간선을 차례로 대입 하면서 트리를 구성하기 때문에 사이클이 이루어지는 확인하면서 진행해야함
- 간선의 개수가 적은 경우에는 크루스칼, 간선의 개수가 많은 경우에는 프림을 사용하는게 효과적이다
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 여러가지 정렬과 시간복잡도 (선택정렬 / 삽입정렬 / 버블정렬 / 퀵정렬 / 힙정렬 / 합병정렬) (0) | 2021.10.21 |
|---|---|
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2021.09.17 |
| [알고리즘] MST - 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2021.09.15 |



댓글